Three Ways to Analyze the Composition of a 90-degree Rotation and a Line Reflection
What is the product of a rotation and a line reflection?
Let R = A90, the rotation by 90 degrees, with center a point A not on m. Let M be line reflection in a line m. If T = MR, what kind of isometry is T and what is it exactly? This product T is an important one, since it occurs in wallpaper patterns that have both 90-degree rotational symmetries and line symmetries.
Here this question is answered in three different ways. The first two of the ways take the knowledge of T from a general theorem about triple line reflections and then trace the images of special points to find T exactly. The third way uses factorization into the product of three line reflections as in the proof of this theorem.
In order to see more clearly where points are located, a coordinate system of squares has been added to the figure with A on the y-axis and m as the x-axis.
Solution Method 1
Since R is a rotation, it is a product of the reflections in two lines intersecting at A. When we take the product with M we get a product of reflections in 3 lines that are not concurrent, so we know that T must be a glide reflection. So the task is to find the invariant line and the glide vector of T. This can be done by finding T(P) for any points P but it is easier to use special choices that are easy to compute.
To begin, find T(A). T(A) = M(R(A)) = M(A) = A', the reflection of A in m.
Next find T(A'). T(A') = M(R(A')) = M(A'') = A''' in the figure. It is easy to see that AA'A''' is an isosceles right triangle.
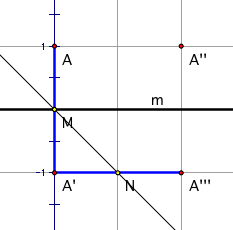
Find the invariant line: The midpoint M of AA' is on m. M and the midpoint N of A'A''' are both on the invariant line, so the invariant line g = line MN, which is parallel to line AA'''. It is a line through M that makes a 45-degree angle with m, as shown.
Find the glide vector: Since M is on the invariant line, the glide vector is MT(M). But since T maps AA' to A'A''' the midpoint of AA' is mapped to the midpoint N of A'A''', so T(M) = N and the glide vector if MN. (It is also possible to see that T(M) = N by first finding R(M) = midpoint AA'' and then reflecting in m to get N.
Note: The glide vector can be found from the image of any point. For example, start with A and its image A' and construct lines through A and A' perpendicular to line MN. The intersections of the perpendiculars with line MN are the centers of two of the squares shown, and the distance between the two intersection points, and their direction, is the same as that of MN.
Solution Method 2
Again we use the knowledge that T is a glide reflection and use the image of special points to find the defining data.
This time put A in the center of a square BCDE, with m = CD.
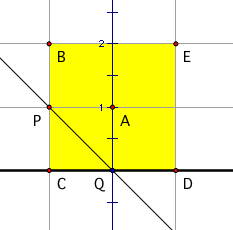
Then T(B) = M(R(B)) = M(C) = C.
Also, TŠ = M(R(C)) = M(D) = D.
Find the invariant line: Let P be the midpoint of BC and let Q be the midpoint of CD. Then the invariant line g passes
through P and Q, so g = line PQ.
Find the glide vector: Observe that T(P) = M(R(P)) = M(Q) =
Q. So the glide vector is PQ since
P is on the invariant line.
Note: The invariant line of a glide
reflection is one special line.
There is no other. But
there are many pairs of points that describe the same vector (and the same
translation, or glide). So both
vector MN from Solution 1 and PQ from solution 2 are the same vectors and are
both glide vectors for T.
Solution Method 3
This method uses 3 mirrors. The rotation R is the product of reflections in two lines meeting with an angle of 45 degrees at A. If we choose the mirror for second reflection to be the line AM perpendicular to m, then the first mirror must be the line AB in the figure. Let reflection in AM be denoted by J and reflection in AB be denoted by K. Thus R = A90 = KJ and T = MR + N(KJ) = (MK)J.
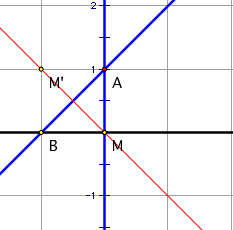
Since AM is perpendicular to m, then MK = the half-turn with
center M. Denote this half-turn by
H. Then T = HJ. These products of half-turns and line
reflections have been studied extensively already and are explored in another
document.
But it is not hard to summarize the results here. The invariant line is the line through
M perpendicular to AB, the mirror line of H.
The glide vector can be found from M and M', its reflection
in AB, for T(M') = HJ(M') = H(M) = M.
So the glide vector is M'M.
What if A is on m?
Look at the methods again. In this case A = M and the 3 mirror lines are concurrent, so by theorem it is known that T is a line reflection. In fact the mirror line is the same line through M as in the cases above, but the glide vector = MM = AA = the zero vector, so T is a line reflection. (You can think of a line reflection as a glide reflection with zero glide vector, but when we categorize isometries into 4 categories, we separate line reflections and glide reflections as two separate categories.)
Self-Test
To check for how well you understand any of these methods, use the same method to analyze S= RM. The process may be made clearer if you use graph paper and make m the x-axis and put A on the y-axis. A second check would be to replace R by the rotation with center A and angle 270 = -90 degrees.
A more difficult task would be to replace R by a rotation by
a different angle such as a multiple of 60 degrees or a general angle.